The Sudoku Game
The origin of this game is due to the Swiss mathematician Leonhard Euler during the eighteenth century. However, it spread its fame in the second half of the 20th century, first in Japan, then spreading to the rest of Asia and the West. Its dissemination and mass use was mainly thanks to the publications of magazines and newspapers, which incorporated the challenges of this game to their readers. Today it is a very popular mathematical game in the world, and its fame has multiplied thanks to internet and mobile applications.
The Board
The game consists of a board with 9 rows and 9 columns, with a total of 81 cells. The board can be further divided into 9 sub-boards or regions of 3 x 3 cells each. In each row, in each column and in each region of this board you have to place the digits from 1 to 9, without repeating them in the same row, column or region.
The board has 9 rows. We number them from 1 to 9. On the right you can see the rows of the board.
There are 362.800 combinations to place de digits 1, 2, 3, 4, 5, 6, 7, 8, 9, without repeating them in the row.
The board has 9 columns. We number them from 1 to 9. On the right you can see the rows of the board.

There are 362.800 combinations to place de digits 1, 2, 3, 4, 5, 6, 7, 8, 9, without repeating them in the column.
The board has 9 regiones or litle squares. Each oh them has 9 cells. En each region you have to fill de digits 1, 2, 3, 4, 5, 6, 7, 8, 9, without repeating them in the region. There are also 362.800 combinations to fill de digits 1, 2, 3, 4, 5, 6, 7, 8, 9, without repeating them in the region.
We call the TOP AREA to the 3 upper regions of the board. We call BOTTOM AREA to the 3 regions bellow. We call LEFT AREA to the 3 regions on the left, and RIGHT AREA to the 3 regions on the right.
Finally, we name the CENTRAL HORIZONTAL AREA to the 3 regions of the central horizontal line and CENTRAL VERTICAL AREA to the 3 regions of the central vertical line.
Below you will find a graphic example showing rows, columns, regions and areas of the 9×9 board. You can try it yourself, by first selecting the button below and then clicking on the board.
Showing rows, columns, regions
Filling the board
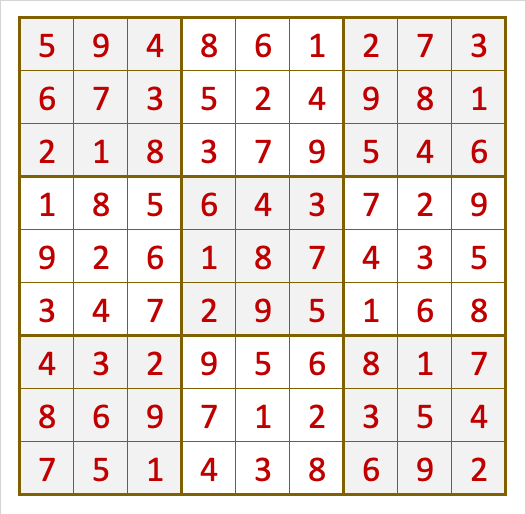
In the Sudoku game the first step is to place the 9 digits from 1 to 9 in the 81 cells of the board, without repeating digits in rows, columns or regions.
When you hav the board with all the numbers correctly arranged, the presentation of the game to solve is to keep some digits visible and hide the rest. So the second step is to hide some cells and show others, in such a way that the user will have to discover the hidden cells, making sure to comply with the rule of not repeating digits in rows, columns or regions. step is the hide some of the digits and show the others

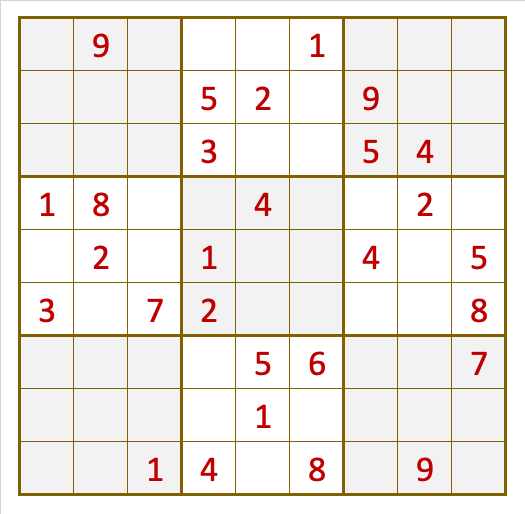
In the example in the image above, we have a set of 28 visible digits and 53 hidden digits.
It is very important that with the visible cells it is possible to solve the presented game, and that the solution is unique (like the one shown in the example).
The greater the number of visible digits, the easier it will be to complete the game. And the smaller the number of visible digits, the more difficult it is to solve. The minimum number of visible digits to ensure that the solution of the game is unique is 17 cells.
Below you will find a graphic example with the board that shows how to randomly fill different rows, columns and regions with the digits 1 to 9, maintaining the rule that they cannot be repeated in rows, columns or regions. You can try it yourself by selecting the button below.
Filling the table
Mistakes
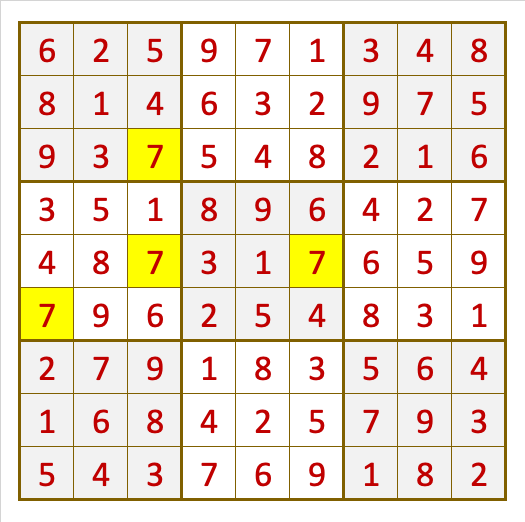
When a repeated digit is found in a row, column or region, it is a mistake or error, as can be seen in the figure.
In this case, in the 3rd column, 5th row, the right digit was the number "2", and it was replaced by the number "7", generating an error repeating that number in the row, the column, and the region (with background color yellow).
There is a nice game in CrossGames21.com, named "5 wrongs" which consists in detecting errors in a board.
Amenities
- The sum of all the numbers in a row is 1+2+3+4+5+6+7+8+9 = 45 (remember the commutative property of addition).
- The sum of all the numbers in a column is also 1+2+3+4+5+6+7+8+9 = 45.
- The sum of all the numbers in a region is also 1+2+3+4+5+6+7+8+9 = 45.
- The sum of all the numbers in the board is 9 * 45 = 405.
Variations
- If you change the order of the rows within the TOP AREA, or within the BOTTOM AREA or within the CENTRAL HORIZONTAL AREA, the result will be a correct board with no errors. The combinations in each area are six (123, 132, 213, 231, 312, 321). So you have 6*6*6=216 variations from a single SUDOKU, taking correct new games.
- Doing the same with vertical areas you have 216 variations too.
- Doing the same moving the complete vertical areas and horizontal areas, you have other 6*6= 36 variations.
- Turning in 90º four times, you have 4 variations too.
- Finally, if you change all the digits "1" by "2" on the board, it will remain a correct new game. So there are 9*8*7*6*5*4*3*2*1 = 9! = 362.800 variations.
- So from 1 game, you can create with this changes, a total of 216 * 216 * 36 * 4 * 362.800 variations, i.e., 2.437.996.216.320 combinations, without errors. It is most likely that many of them are the same as others, but even so, it is clear that multiple games can be generated from one game
Changing order of rows/columns out of their areas
If you change the order of rows or columns, moving them out of their areas (horizontal or vertical), it will generate a board with errors, doubling digits in rows, columns or regions.
There are two nice games in CrossGames21.com, named "Castling" and "Drag & Drop", which consists in detecting errors in a board where 2 rows where moved out of their respective areas, and the challenge is to detect them and fix de game.
Hidden and Visible digits
When you hav the board with all the numbers correctly arranged, the presentation of the game to solve is to keep some digits visible and hide the rest.


In the example in the image above, we have a set of 28 visible digits and 53 hidden digits.
It is very important that with the visible cells it is possible to solve the presented game, and that the solution is unique (like the one shown in the example).
The greater the number of visible digits, the easier it will be to complete the game. And the smaller the number of visible digits, the more difficult it is to solve. The minimum number of visible digits to ensure that the solution of the game is unique is 17 cells.
Games with more than one solution
In many cases, certain combinations of visible digits could generate more than one solution for the game. And many times multiple solutions.
In the following example, the game has 2 possible solutions
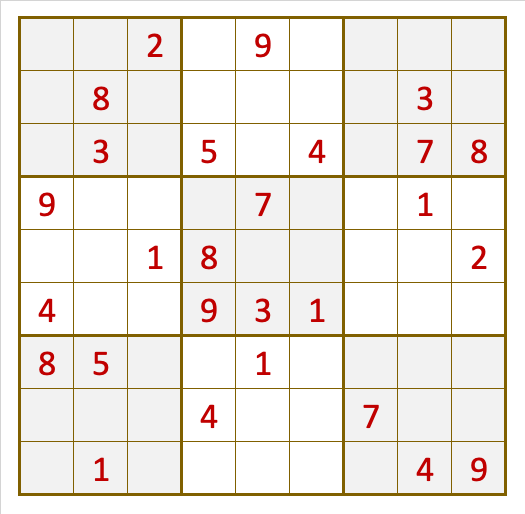

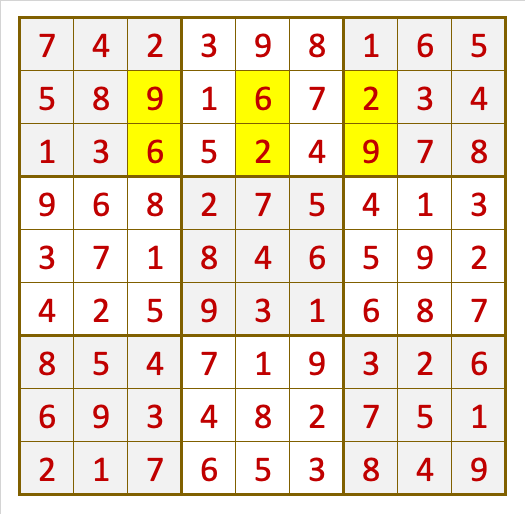
As can be seen, it is possible to advance with 75 of the 81 cells, whose solution is unique. However, for the last 6 cells, with yellow background, there are 2 different solutions. In the second row, numbers 6, 2 and 9 can be placed, but they can also be the numbers 9, 6 and 2. In the first case, in the third row, the numbers must be 9, 6 and 2. In the second case, in the third row, the numbers must be 6, 2 and 9.
So we have 2 solutions for this game. In our website, all games have a unique solution.
Other sizes
There are different board sizes in Sudoku games. The most used is the 9x9, which is the one we develop on this website.
However there are other sizes, the best known are:



The 4x4 size uses the digits 1,2,3 and 4. The 6x6 size uses the digits 1,2,3,4,5 and 6. The 16x16 size uses de hexadecimal digits from 1 to 16.
Other symbols and figures
In some cases, especially in 4x4, it is common to see games where digits are changed for figures, animals, objects, etc. For children is a good idea.
However, when abstract symbols are used, the difficulty can be very high



Words in Sudoku
The use of words in Sudoku games is a new option in Sudoku games. In this case, the 9 letters of the word are placed in each row, column and region.
In the figure, we can see de word SINGAPORE in the highlighted row.

Other topics
| CrossGames21 | Presentation |
| The Sudoku Game | Explanation of the sudoku game |
| Games | Explanation of all games in CrossGames21.com |
| Levels | Difficulty levels of the games |
| Rules | Use of options / board and keyboard in CrossGames21.com |
| Techniques | Tricks to solve sudoku games |
| Statistics | Statistics of games in CrossGames21.com |